数据结构
1.1抽象数据类型的表现与实现
Section titled “1.1抽象数据类型的表现与实现”抽象数据类型的实现
ADT{ Data 数据对象的定义 数据元素之间逻辑关系的定义 Operation 操作一 初始条件 操作结果描述 操作n ...}ADT typename
ADT Complex{ D = {r1,r2 | r1,r2都是实数} S = {<r1,r2> | r1实部,r2虚部} assign(&C,v1,v2) 初始条件:空的复数已存在 操作结果:赋值给C destory(&C)}void assign(Complex *A,float real,float imag){//复数赋值 A->realpart = real; //实部赋值 A->imagpart = imag;}void add(Complex *C,Complex A,Complex B){ C->realpart = A.realpart + B.realpat; /*实部相加*/ C->imagpart = A.imagpart + B.imagpart;}1.2算法和算法分析
Section titled “1.2算法和算法分析”算法特性:有穷性 确定性 可行性 0或多个输入 至少1个输出
\1. 输入:一个算法应以待解决的问题的信息作为输入。
\2. 输出:输入对应指令集处理后得到的信息。
\3. 可行性:算法是可行的,即算法中的每一条指令都是可以实现的,均能在有限的时间内完成。
\4. 有穷性:算法执行的指令个数是有限的,每个指令又是在有限时间内完成的,因此整个算法也是在有限时间内可以结束的。
\5. 确定性:算法对于特定的合法输入,其对应的输出是唯一的。即当算法从一个特定输入开始,多次执行同一指令集结果总是相同的。
算法设计要求:正确性Correctness 可读性Readability 健壮性Robustness 高效性Efficiency
2.1线性表
Section titled “2.1线性表”顺序表 线性表的顺序表示
Section titled “顺序表 线性表的顺序表示”顺序表的基本概念
概念:用一组地址连续的存储单元依次存储线性表的数据元素,这种存储结构的线性表称为顺序表。
特点:逻辑上相邻的数据元素,物理次序也是相邻的。
1、顺序表时间复杂度 从以上代码可以很明显的看出,线性表的顺序存储结果在读、存数据是的时间复杂度是O(1),插入、删除操作的时间复杂度是O(n)。
2、顺序表的优缺点 优点:无须为表中元素之间的逻辑关系而增加额外的存储空间;可以快速的存取表中任一位置的元素。
缺点:插入和删除操作需要移动大量元素;当线性表长度较大时,难以确定存储空间的容量;造成存储空间的“碎片”。
存取结构
1.1随机存取 随机存取(直接存取,Random Access)指的是当存储器中的数据被读取或写入时,所需要的时间与该数据所在的物理地址无关。
随机存取的微观现实例子就是编程语言中的数组。 随机存取的宏观现实例子就是我们的随机存取存储器(RAM:Random Access Memory),通俗的说也就是我们电脑的内存条。因为RAM利用电容存储电荷的原理保存信息,所以RAM可以高速存取,且与物理地址无关。
1.2顺序存取 顺序存取(Sequential Access)是一种按记录的逻辑顺序进行读、写操作的存取方法,所需要的时间与该数据所在的物理地址有关。顺序存取表现为:在存取第N个数据时,必须先访问前(N-1)个数据。 顺序存取的微观现实例子就是数据结构中的链表。 顺序存取的现实例子就是我们的录音磁带、光盘、机械硬盘里面的磁盘。磁带、光盘、磁盘上的数据分别存储在不同扇区、不同磁道上,磁盘的读写磁头通过切换不同扇区和磁道来读取物理地址不连续的数据时,该过程中要经过不同扇区和不同磁道上的无关数据,磁盘的读写磁头在切换不同扇区和磁道所需时间也不同,故为顺序存取。
存储结构
顺序存储 数组
链式存储 单链表
索引存储 索引表
哈希存储 哈希表
基本操作


#include<stdio.h>#include<stdlib.h>
#define MAXSIZE 20 //线性表存储空间的初始分配量#define OK 1 //成功标识#define ERROR 0 //失败标识
typedef int Status; //Status是函数的类型,其值是函数结果状态代码,如OK等typedef int ElemType;typedef struct{ ElemType *elem; int length; //数组长度}SqList;//操作//初始化 创建一个空的顺序表Status InitList(SqList* L){ L->elem = (ElemType*)malloc(sizeof(ElemType)*MAXSIZE); if(!L->elem){ return ERROR; } L->length = 0; return OK;}//插入 在第i个位置插入ElemType eStatus ListInsert(SqList* L,int i,ElemType e){ int k; if(L->length == MAXSIZE) return ERROR; if(i < 1 || i > L->length + 1) return ERROR; if (i < L->length + 1){ for(k = L->length-1;k >= i-1;k--){ L->elem[k+1] = L->elem[k]; } //elem[i] = elem[i-1] } L->elem[i-1] = e; L->length ++; return OK;}//删除第i个元素,将元素的值传给eStatus ListDelete(SqList* L,int i,ElemType *e){ if(L->length == 0) return ERROR; if(i < 1 || i >L->length) return ERROR; int k; *e = L->elem[i-1]; if(i < L->length){ for(k = i- 1; k <= L->length - 2;k++){//max{k+1} = length - 1 L->elem[k] = L->elem[k+1]; } } L->length--; return OK;}//获取某一位置上的元素Status GetElem(SqList L,int i,ElemType *e){ if(i < 1 || i > L.length) return ERROR; *e = L.elem[i-1]; return OK;}//查找某一个元素的位置,将位置传给*iStatus LocateElem(SqList L,ElemType e,int *i){ int k; for (k = 0;k < L.length;k++){ if(L.elem[k] == e){ *i = k + 1; return OK; } } if(k == L.length - 1){ printf("不存在e"); return ERROR; }}//读取顺序表的所有元素void Output(SqList L){ printf("当前顺序表的长度为:%d\n",L.length); for(int i = 0; i < L.length;i++){ printf("%d ",L.elem[i]); } printf("\n");}//运行测试int main(){ SqList L; ElemType e; int i; printf("创造一个空的线性表L\n"); InitList(&L); Output(L); for(int i = 0 ; i <= 10; i++){ ListInsert(&L,i,i); //length = 11 } Output(L); printf("在第三位插入0\n"); ListInsert(&L,3,0); Output(L); ListDelete(&L,6,&e); printf("删除的数据为%d\n",&e); Output(L); printf("查找元素10\n"); e = 10; LocateElem(L,e,&i); printf("查找到e在第%d位置\n",&i); printf("------获取元素操作------\n"); GetElem(L,5,&e); printf("得到第5个元素:%d\n", e);}线性表的链式存储结构
Section titled “线性表的链式存储结构”在链式结构中,除了要存储数据元素的信息外,还要存储它的后继元素的存储地址。因此,为了表示每个数据元素ai与其直接后继元素ai+1之间的逻辑关系,对数据ai来说,除了存储其本身的信息之外,还需要存储一个指示其直接后继的信息(即直接后继的存储位置)。我们吧把存储数据元素信息的域称为数据域,把存储直接后继位置的域称为指针域。指针域中存储的信息称做指针或链。这两部分信息组成数据元素ai的存储映像,称为结点(Node)。 n个结点(ai的存储映像)链结成一个链表,即为线性表(a1, a2, …, an)的链式存储结构,因为此链表的每个结点中只包含一个指针域,所以叫做单链表。
在C语言中,当我们需要修改指针所指向的内存区域时,就需要使用二重指针。对于链表来说,当我们需要修改链表头指针的内容时,就需要使用二重指针。因为链表头指针是一个指向链表头节点的指针,如果直接传递链表头指针作为参数到函数中,那么在函数内部修改链表头指针的内容并不会影响到外部的链表头指针。因此,我们需要传递一个指向链表头指针的指针(即二重指针),这样就可以在函数内部修改链表头指针的内容,并且这个修改会影响到外部的链表头指针。
//操作p = L; //p为头指针L,指向头结点p = L->next; //p为头结点,p指向首元结点p = p->next;//p指向下一结点头插法&尾插法
//头插法p->next = L->next;L->next = p;//尾插法L->next = pL = p;//--------------create list from head--------Status HeadInsert(LinkList* L,int n){ if(n < 1) return ERROR; Node* headNode = (Node*)malloc(sizeof(Node)); headNode->next = NULL; (*L)->next = headNode; int i = 1; while(i <= n){ Node* p = (Node*)malloc(sizeof(Node)); scanf("%d",&p->data); p->next = headNode->next; headNode->next = p; i++; } (*L)->length = i; return OK;}//---------create list from tail--------Status TailInsert(LinkList* L,int n){ if(n < 1) return ERROR; Node* tailNode = (Node*)malloc(sizeof(Node)); tailNode = (*L); int i = 1; while(i <= n){ Node* p = (Node*)malloc(sizeof(Node)); scanf("%d",&p->data); tailNode->next = p; tailNode = p; i++; } tailNode->next = NULL; (*L)->length = i; return OK;}//打印有头结点的链表void OutPut(LinkList L){//L->next 为头节点,不储存数据 Node* p = L->next->next; for(int i = 0;i < L->length;i++){ printf("%d\n",p->data); p = p->next; }}//打印无头结点的列表void OutPut2(LinkList L){//无头结点,有尾结点 Node* p = L->next; for(int i = 0;i < L->length;i++){ printf("%d\n",p->data); p = p->next; }}//testint main(){ int num; LinkList L1,L2; // printf("请输入头插的元素个数:"); // scanf("%d",&num); // HeadInsert(&L1,num); // printf("头插结果为:\n"); // OutPut(L1);
printf("请输入尾插的元素个数:"); scanf("%d",&num); TailInsert(&L2,num); printf("尾插结果为:\n"); OutPut2(L2); return 0;}



#include <stdio.h>#include <stdlib.h>#define OK 1#define ERROR 0typedef int Status;typedef int ElemType;//构造节点typedef struct Node{ ElemType data; struct Node *next;}Node;//构造单链表typedef struct linklist{ int length; Node *next;}ListNode,*LinkList;//初始化单链表//LinkList 是指向头结点的指针,LinkList*为指向该指针的指针。此处传入LinkList L的地址,目的是修改L的指向。Status InitList(LinkList *L){ LinkList p = (LinkList)malloc(sizeof(LinkList)); Node *q = (Node*)malloc(sizeof(Node)); //头节点 一般不储存数据值 (这样就不会在每次建立节点时给出数据值) q->next = NULL; p->next = q; //头指针指向头节点 p->length = 0; (*L) = p; //将头指针传递给变量 *L return OK;}//判断是否为空链表int IsEmpty(LinkList L){ if(L->next->next) return OK; else return ERROR;}//单链表的插入Status InsertList(LinkList *L,int pos,ElemType e){ if(pos < 1 || pos > (*L)->length+1) return ERROR; //插入位置可以是1 到 length +1 Node *p = (*L)->next; //头节点 for(int i = 1; i <= pos-1; i++){ p = p->next; } //从 p -- p->next 变为 p -- q -- p->next Node *q = (Node*)malloc(sizeof(Node)); q->data = e; q->next = p->next; p->next = q; (*L)->length++; return OK;}//单链表的删除Status ListDelete(LinkList *L,ElemType *elem,int pos){ if(pos < 1 || pos > (*L)->length) return ERROR; Node *p = (*L)->next; Node *q; for(int i = 1; i < pos; i++){ p = p->next; } q = p->next; p->next = q->next; free(q); (*L)->length--; return OK;}//清空单链表 保留头结点,头指针Status Clear(LinkList *L){ Node* p = (*L)->next->next,*q;//L->next->next为首元结点,即第一个存放数据的结点 while(p != NULL){ q = p; free(q); p = p->next; } (*L)->next->next = NULL; (*L)->length = 0; return OK;}//销毁单链表 将头结点,头指针全部销毁Status DestoryList(LinkList *L){ Node* p = (*L)->next,*q;//p为头结点 while(p){ q = p; p = p->next; free(q); } free((*L)); // (*L)是指向链表表头的指针,free释放指针占用的内存 (*L) = NULL; //指针内存释放之后,手动将其设置为NULL,避免出现野指针 //野指针:指向已经释放的内存区域的指针 return OK;}//遍历打印单链表void OutPut(LinkList L){//L->next 为头节点,不储存数据 Node* p = L->next->next; for(int i=0;i<L->length;i++){ printf("%d ",p->data); p = p->next; } printf("\n"); //换行符显示}//testint main(){ LinkList L; InitList(&L); printf("------测试插入10个数------\n"); for(int i = 1; i<=10;i++){ InsertList(&L,i,i); } OutPut(L); printf("------删除第5位的数据------\n"); ElemType elem; ListDelete(&L, &elem, 5); OutPut(L); printf("------清空单链表------\n"); Clear(&L); OutPut(L);}1、静态链表的基本概念
Section titled “1、静态链表的基本概念”静态链表,使用数组连描述指针,首先我们让数组的元素都是由两个数据域组成,data和cur。数据域data,用来存放数据元素;游标cur相当于单链表的next指针,存放该元素的后继在数组中的下标。
另外我们对数组的第一个和最后一个元素作为特殊元素处理,不存数据。通产把未被使用的数组元素称为备用链表。而数组第一个元素,即下标为0的元素的cur存放备用链表的第一个结点的下标;而数组的最后一个元素的cur则存放第一个有数值的元素的下标,相当于单链表中的头结点的作用,当整个链表为空时,则为0
#include <stdio.h>#include <stdlib.h>#define MAXSIZE 1000#define ERROR 0#define OK 1typedef int Status;typedef int ElemType;
typedef struct{ ElemType data; int cur; //游标CUrsor 为0时表示无指向}Component,StaticLinkList[MAXSIZE];//未被使用的数组元素称为备用链表//数组最后一个元素的cur存放第一个有数值的元素的下标,相当于头结点//数组的第一个元素的cur存放备用链表的第一个元素的下标Status InitList(Component *space){ for(int i=0;i<MAXSIZE;i++){ space[i].cur = i+1; //space[0].cur = 1 } space[MAXSIZE-1].cur = 0;//0表示空指针,目前静态链表为空 return OK;}//申请下一个分量的资源 返回值为链表中第一个可用空间的索引int Malloc_SLL(StaticLinkList space){ int i = space[0].cur; if(space[0].cur != 0 ){ space[0].cur = space[i].cur; } return i;}//释放分量的资源void Free_SLL(StaticLinkList space,int i){ space[i].cur = space[0].cur; space[0].cur = i;}//得到链表的长度int ListLength(StaticLinkList L){ int j = 0; int i = K[MAXSIZE-1].cur; while(i){ i = L[i].cur; j++; } return j;}//插入Status ListInsert(Component *L,int i,ElemType e){ int j,k,l; k = MAXSIZE - 1; if(i < 1 || i > ListLength(L) + 1) return ERROR; j = Malloc_SLL(L); if(j){ L[j].data = e; for(l = 1;l <= i-1;l++){ k = L[k].cur; } L[j].cur = L[k].cur; L[k].cur = j; return OK; } return ERROR;}//删除Status ListDelete(Component *L,int i,ElemType *e){ int j,k; if(i < 1 || i > ListLength(L)) return ERROR; k = MAXSIZE - 1; for(j = 1;j <= i-1;j++){ k = L[k].cur; } j = L[k].cur; L[k].cur = L[j].cur; *e = L[j].data; Free_SLL(&L,j); return OK;}循环链表的基本概念
将单链表中终端节点的指针端由空指针改为指向头结点,就使整个单链表形成一个环,这种头尾相接的单链表称为单循环链表,简称循环链表。
tips:循环链表的尾指针一般指向链表的最后一个节点,尾指针的next指向链表的第一个节点。头指针指向链表的第一个节点。



合并两个循环链表(仅设尾结点)
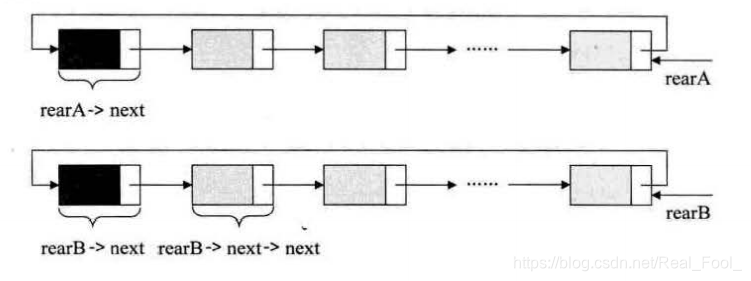
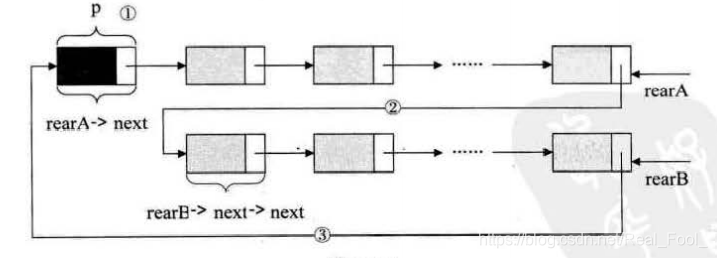
//只保存A的头结点 rearA->next;p = rearA->next;//将rearA尾指针指向B的首个存放数据的结点,rearB->next->nextrearA->next = rearB->next->next;//reatB指向A的头结点rearB->next = p;//释放pfree(p);typedef struct DulNode{ ElemType data; DulNode* prior; DulNode* next;}DulNode,*DulNodeList;//插入 s 到 p 之前s->prior = p->prior;s->next = p;p->prior->next = s;p->prior = s;//插入s 到 p 之后s->prior = p;s->next = p->next;p->next = s;p->next->prior = s;//删除p->next = q->next->next;q->next->prior = p;free(q);3.1栈与队列
Section titled “3.1栈与队列”
栈stack
Section titled “栈stack”栈(Stack):是只允许在一端进行插入或删除的线性表。首先栈是一种线性表,但限定这种线性表只能在某一端进行插入和删除操作。
栈顶(Top):线性表允许进行插入删除的那一端。 栈底(Bottom):固定的,不允许进行插入和删除的另一端。 空栈:不含任何元素的空表。
栈又称为后进先出(Last In First Out)的线性表,简称LIFO结构

基本操作
初始化 判断是否为空 进出栈
读取栈顶 销毁栈
栈的顺序存储结构
Section titled “栈的顺序存储结构”采用顺序存储的栈称为顺序栈,它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素,同时附设一个指针(top)指示当前栈顶元素的位置。 若存储栈的长度为StackSize,则栈顶位置top必须小于StackSize。当栈存在一个元素时,top等于0,因此通常把空栈的判断条件定位top等于-1。

#define MAXSIZE 50#define OK 1#define ERROR 0typedef int ElemType;typedef int Statustypedef struct stack{ ElemType data[MAXSIZE]; int top; //用于栈顶指针}SqStack;//初始化void InitStack(SqStack* S){ S->top = -1;}//判断栈空bool IsEmpty(SqStack S){ if(S.top == -1) return true; else return false;}//进栈Status Push(Stack* S,ElemType e){ if(S->top == MAXSIZE-1) return ERROR; S->top++; S->data[S->top] = e; return OK;}//出栈Status Pop(SqStack *S,ElemType *e){ if(S->top == -1) return ERROR; *e = S->data[S->top]; S->top--; return OK;}//获取栈顶元素Status GetTop(SqStack S,ElemType *e){ if(S->top == -1) return ERROR; *e = S>data[S->top];}共享栈
top0 == -1 零号栈为空
top1 == MAXSIZE 1号栈为空
top0 + 1 == top1 栈满

#define MAXSIZE 50#define int ElemType#define int Status#define OK 1#define ERROR 0typedef struct{ ElemType data[MAXSIZE]; int top0; //栈0栈顶指针 int top1; //栈1栈顶指针}SqDoubleStack;//进栈Status Push(SqDoubleStack *S,ElemType e,int stackNumber){ if(S->top0 + 1 == S->top1) return ERROR; if(stackNumber == 0){//进入0号栈 S->data[++S->top0] = e; }else if(stackNumber == 1){//进入1号栈 S->data[--S->top1] = e; } return OK;}//出栈Status Pop(SqDoubleStack *S,ElemType e,int stackNUmber){ if(stackNumber == 0){ if(S->top0 == -1) return ERROR; *e = S->data[S->top0--]; //*e赋值为data[S->top0],并让top0自减 }else if(stackNumber == 1){ if(S->top1 == MAXSIZE) return ERROR; *e = S->data[S->top1++]; } return OK;}栈的链式存储结构
Section titled “栈的链式存储结构”采用链式存储的栈称为链栈,链栈的优点是便于多个栈共享存储空间和提高其效率,且不存在栈满上溢的情况。通常采用单链表实现,并规定所有操作都是在单链表的表头进行的。这里规定链栈没有头节点,Lhead指向栈顶元素
链表为空其实就是top = NULL

//构造结点typedef struct StackNode{ ElemType data; struct StackNode* next;}StackNode,*LinkStackPrt;//构造链栈typedef struct LinkStack{ LinkStackPrt top; int count}LinkStack;//进栈Status Push(LinkStack *S,ElemType e){ LinkStackPrt p = (LinkStackPrt)malloc(sizeof(StackNode)); p->data = e; p->next = S->top; S->top = p; S->count++; return OK;}//出栈Status Pop(LinkStack *S,ElemType *e){ if(S->top == NULL) return ERROR; LinkStackPrt p; *e = S->top->data; p = S->top; S->top = S->top->next; free(p); S->count--; return OK;}栈的应用——递归
Section titled “栈的应用——递归”递归的定义
递归是一种重要的程序设计方法。简单地说,若在一个函数、过程或数据结构的定义中又应用了它自身,则这个函数、过程或数据结构称为是递归定义的,简称递归。
必须注意递归模型不能是循环定义的,其必须满足下面的两个条件
- 递归表达式(递归体)
- 边界条件(递归出口)
①斐波那契数列
Section titled “①斐波那契数列”在递归调用的过程中,系统为每一层的返回点、局部变量、传入实参等开辟了递归工作栈来进行数据存储,递归次数过多容易造成栈溢出等。而其效率不高的原因是递归调用过程中包含很多重复的计算。下面以n=5为例,列出递归调用执行过程,如图所示:
如图可知,程序每往下递归一次,就会把运算结果放到栈中保存,直到程序执行到临界条件,然后便会把保存在栈中的值按照先进后出的顺序一个个返回,最终得出结果。

int Fibonacci(int n){ if(n == 0){ return 0;//边界条件 }else if(n == 1){ return 1;//边界条件 }else{ return Fibonacci(n-1) + Fibonacci(n-2);//递归表达式 }}②四则运算表达式求值
Section titled “②四则运算表达式求值”后缀表达式计算结果
后缀表达式的运算符在操作数后面,在后缀表达式中已考虑了运算符的优先级,没有括号,只有操作数和运算符。
例如中缀表达式转后缀表达式 (逆波兰式)
A + B ∗ ( C − D ) − E / F
对应的后缀表达式为
A B C D − ∗ + E F / − 步骤
① (( A + (B ∗ ( C − D ))) − (E / F)) 给每一个表达式按顺序用括号括起来
②**( A ( B ( C D ) - ) * + ( E F )) / -** 将运算符移到括号右边 若要转为前缀表达式(波兰式)则移到左边
③**A B C D − ∗ + E F / −**去括号

逆波兰式即为下列二叉树的后序遍历

如何实现后缀表达式求值?
后缀表达式计算规则:从左到右遍历表达式的每个数字和符号,遇到是数字就进栈,遇到是符号,就将处于栈顶两个数字出栈,进行运算,运算结果进栈,一直到最终获得结果。
如何将中缀表达式转为后缀表达式
规则:从左到右遍历中缀表达式的每个数字和符号,若是数字就输出,即成为后 缀表达式的一部分;若是符号,则判断其与栈顶符号的优先级,是右括号或优先级低于栈顶符号(乘除优先加减)则栈顶元素依次出栈并输出,并将当前符号进栈,一直到最终输出后缀表达式为止。
队列Queue
Section titled “队列Queue”1、队列的定义 队列(queue)是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。 队列是一种先进先出(First In First Out)的线性表,简称FIFO。允许插入的一端称为队尾,允许删除的一端称为队头。
队头(Front):允许删除的一端,又称队首。 队尾(Rear):允许插入的一端。 空队列:不包含任何元素的空表。

队列的存储结构
Section titled “队列的存储结构”初始状态(队空条件):Q->front == Q->rear == 0 进队操作:队不满时,先送值到队尾元素,再将队尾指针加1。 出队操作:队不空时,先取队头元素值,再将队头指针加1。
#define MAXSIZE 50typedef int ElemTypetypedef struct{ ElemType data[MAXSIZE]; int front; int rear;}SqQueue;图(d)中队列出现“假溢出”

初始Q->front = Q->rear = 0
队首指针进1(出队) Q->front = (Q->front + 1) % MAXSIZE
**队尾指针进1 (入队)**Q->rear = (Q->rear + 1) % MAXSIZE
队列长度(Q->rear - Q->front + MAXSIZE) % MAXSIZE

typedef struct{ ElemType data[MAXSIZE]; int front;//头指针 int rear;//尾指针,若队列不空,指向队列尾元素的下一个位置}SqQueue;//队列的初始化Status InitQueue(SqQueue *Q){ Q->front = 0; Q->rear = 0; return OK;}//判断队列是否为空Status isEmpty(SqQueue Q){ if(Q.rear == Q.front) return true; else return false;}//判断队列是否已满,通过少占用一个空间,因为Q->rear == Q->front时不一定队满Status isFull(SqQueue Q){ if((Q.rear + 1) % MAXSIZE = Q.front) return OK; else return ERROR;}//求循环队列的长度int QueueLength(SqQueue Q){ //如果rear走到front前面,Q.rear + MAXSIZE - Q.front 即为Queue的长度 return (Q.rear - Q.front + MAXSIZE) % MAXSIZE;}//循环队列入队Status EnQueue(SqQueue *Q,ElemType e){ //如果队列已满则返回ERROR //if((Q->rear + 1) % MAXSIZE == Q->front) return ERROR; if(isFull(*Q)) return ERROR; Q->data[Q->rear] = e; Q->rear = (Q->rear + 1) % MAXSIZE; return OK;}//循环队列出队Status DeQueue(SqQueue *Q,ElemType *e){ if(isEmpty(*Q)) return ERROR; *e = Q->data[Q->front]; Q->front = (Q->front + 1) % MAXSIZE; return OK;}//取对头元素ElmeType GetHead(SqQueue Q){ if(Q.front != Q.rear){ return Q.data[front]; }}队列的链式存储结构表示为链队列,它实际上是一个同时带有队头指针和队尾指针的单链表,只不过它只能尾进头出而已。
头结点一般不存储数据

#define MAXSIZE 100
typedef struct Qnode{ ElemType data; struct Qnode *next;}LinkNode;
typedef struct{ LinkNode* front; LinkNode* rear;}LinkQUeue;//链队列的初始化Status InitQueue(LinkQueue *Q){ Q->front = Q->rear = (LinkNode)malloc(sizeof(Qnode)); Q->front->next = NULL; return OK;}//进队Status EnQueue(LinkQueue *Q,ElemType e){ LinkNode s = (LinkNode)malloc(sizeof(LinkNode)); s->data = e; s->next = NULL; Q->rear->next = s; Q->rear = s; return OK;}//出队Status DeQueue(LinkQueue *Q,ElemType *e){ if(Q->front == Q->rear) return ERROR; LinkNode p = Q->front->next;//要被free的结点 *e = p->data; Q->front->next = p->next; if(Q->rear == p){//如果p是对位 Q->rear = Q->front; } free(p); return OK;}//销毁Status DestoryQueue(LinkQueue *Q){ while(Q->front){ p = Q->front->next; free(Q.front); Q->front = p; } return OK;}双端队列是指允许两端都可以进行入队和出队操作的队列,如下图所示。其元素的逻辑结构仍是线性结构。将队列的两端分别称为前端和后端,两端都可以入队和出队。

特殊的双端队列
输出受限

输入受限

4.1串,数组,广义表
Section titled “4.1串,数组,广义表”串(string)
Section titled “串(string)”
Definition
空串:n = 0时的串称为空串。 空格串:是只包含空格的串。空格串是有内容有长度的,而且可以不止一个空格。 子串与主串:串中任意个数的连续字符组成的子序列称为该串的子串,包含子串的串称为主串。 子串在主串中的位置子串的第一个字符在主串中的序号。
串相等 字符和长度均相同
串的存储结构
Section titled “串的存储结构”定长顺序存储表示SString :类似于线性表的顺序存储结构,用一组地址连续的存储单元存储串值的字符序列。在串的定长顺序存储结构中,为每个串变量分配一个固定长度的存储区,即定长数组。
堆分配存储表示HString :堆分配存储表示仍然以一组地址连续的存储单元存放串值的字符序列,但它们的存储空间是在程序执行过程中动态分配得到的
在C语言中,存在一一个称之为“堆”的自由存储区,并用malloc()和free()函数来完成动则返回一个指向起始地址的指针,作为串的基地址,这个串由ch指针来指示;若分配失败,则返回NULL。已分配的空间可用free()释放掉。 上述两种存储表示通常为高级程序设计语言所采用。块链存储表示仅做简单介绍。 块链存储表示:类似于线性表的链式存储结构,也可采用链表方式存储串值。由于串的特殊性(每个元素只有一个字符),在具体实现时,每个结点既可以存放一个字符, 也可以存放多个字符。每个结点称为块,整个链表称为块链结构
图(a)是结点大小为4 (即每个结点存放4个字符)的链表,最后一个结点占不满时通常用“#”补上;图(b)是结点大小为1的链表。

串的基本操作
Section titled “串的基本操作”StrAssign(&T, chars): 赋值操作。把串T赋值为 chars Strcopy(&T, S): 复制操作。由串S复制得到串T。 StrEmpty(S): 判空操作。若S为空串,则返回TRUE,否则返回 FALSE StrCompare(S,T): 比较操作。若S>T,则返回值>0;若S=T,则返回值=0;若S<T,则返回值<0。 StrEngth(S): 求串长。返回串S的元素个数 Substring(&Sub,S,pos,1en):求子串。用Sub返回串S的第pos个字符起长度为len的子串。 Concat(&T,S1,S2): 串联接。用T返回由S1和S2联接而成的新串。 Index(S,T): 定位操作。若主串S中存在与串T值相同的子串,则返回它在主串S中第一次出现的位置;否则函数值为0 Clearstring(&S): 清空操作。将S清为空串 Destroystring(&S): 销毁串。将串S销毁 不同的高级语言对串的基本操作集可以有不同的定义方法。在上述定义的操作中,串赋值StrAssign、串比较 StrCompare、求串长 Strength、串联接 Concat及求子串 Substring五种操作构成串类型的最小操作子集,即这些操作不可能利用其他串操作来实现;反之,其他串操作(除串清除 Clearstring和串销毁 Destroystring外)均可在该最小操作子集上实现。 例如,可利用判等、求串长和求子串等操作实现定位函数 Index(S,T)。
//定长顺序存储表示#define MAXLEN 255typedef struct{ char ch[MAXLEN]; int length;}SString;//堆分配存储表示typedef struct{ char *ch; int length;}HString;//块链结构#define CHUNKSIZE 80typedef struct Chunk{ char ch[CHUNKSIZE]; struct Chunk* next;}Chunk;typedef struct{ Chunk *head,*tail;//串的头指针和尾指针 int curlen;}LString;串的模式匹配算法
Section titled “串的模式匹配算法”①BF算法(Brute-Force),简单匹配算法
时间复杂度O(n*m)
int Index(SString S,SString T){//目标串S模式串T int i = 0,j = 0; while(i < S.length && j < T.length){ if(S.ch[i] == T.ch[i]){ i++;j++; }else{ //T从0位置移到到j位置,移动了j个长度 //同样的,i也移动了j个长度 //i要回到原来的位置,则i = i - j //回到原来位置后,向右移动一个长度 //i = i- j + 1 i = i - j + 1; j = 0; } } if(j == T.length){//匹配成功,返回S中子串的位置, S移动了T.length - 1个长度 return i - T.length + 1; }else{ return -1; }}②KMP算法,快速匹配算法
KMP算法流程
假设目标串S匹配到i位置,模式串T匹配到j位置
如果j = -1,或者当前字符匹配成功(即S[i] == P[j]),都令i++,j++,继续匹配下一个字符; 如果j != -1,且当前字符匹配失败(即S[i] != P[j]),则令 i 不变,j = next[j]。此举意味着失配时,模式串P相对于文本串S向右移动了j - next [j] 位。 换言之,当匹配失败时,模式串向右移动的位数为:失配字符所在位置 - 失配字符对应的next 值,即移动的实际位数为:j - next[j],且此值大于等于1。
int KMPsearch(char* s,char *p){ int i = 0; int j = 0; int sLen = strlen(s); int pLen = strlen(p); while(i < sLen && j < qLen){ if(j == 0 || s[i] == p[j]){ i++;j++; }else{//j != -1 j = next[j]; } } if(j = pLen) return i-j; else return -1;}数组(Array)
Section titled “数组(Array)”基本操作:InitArray(A,n,bound1,…,boundn)// 若维数n和各维的长度合法,则构造相应的数组A,并返回TRUE;DestroyArray(A)//销毁数组A;GetValue(A,e, index1, …,indexn)// 若下标合法,用e返回数组A中由index1, …,indexn所指定的元素的值。SetValue(A,e,index1, …,indexn)//若下标合法,则将数组A中由index1, …,indexn所指定的元素的值置为e。

三元组表示法
Section titled “三元组表示法”typedef struct{ int row,col; ElemType e;}Triple;typedef struct{ Triple data[MAXSIZE]; int m,n,len;//矩阵的行数,列数,非零元素个数}TSMatrix;//转置void TransMatrix(ElementType source[n][m],ElementType dest[m][n]){ int i,j; for(i = 0;i < m;i++){ for(j = 0;j < n;j++){ dest[i][j] = source[j][i]; } }}稀疏矩阵的链式存储结构——十字链表
Section titled “稀疏矩阵的链式存储结构——十字链表”十字链表
#define MAX_VERTEX_NUN 20typedef char VertexData;//弧结点typedef struct ArcNode{ int tailvex,headvex; struct ArcNode* hlink,*tlink;}ArcNode;//顶点结构typedef struct VertexNode{ VertexData data; ArcNode *firstin,*firstout;}VertexNode;//十字链表结构typedef struct{ VertexNode vertex[MAX_VERTEX_NUM]; int vexnum,arcnum;}OrthList;基本运算
求表头
GetHead(L); //非空广义表的第一个元素,表头可以是一个表。
求表尾
GetTail(L); //非空广义表除去表头元素以外的其他元素所构成的表,表尾一定是一个表。
图Graph
Section titled “图Graph”注意:线性表可以是空表,树可以是空树,但图不可以是空图。就是说,图中不能一个顶点也没有,图的顶点集V一定非空,但边集E可以为空,此时图中只有顶点而没有边。
图中的概念和基本术语
Section titled “图中的概念和基本术语”若E是有向边(也称弧)的有限集合时,则图G为有向图。弧是顶点的有序对,记为<v, w>,其中v,w是顶点,v称为弧尾,w称为弧头,<v,w>称为从顶点v到顶点w的弧,也称v邻接到w,或w邻接自v。

若E是无向边(简称边)的有限集合时,则图G为无向图。边是顶点的无序对,记为(v, w)或(w,v),因为(v,w)=(w,v), 其中v,w是顶点。可以说顶点w和顶点v互为邻接点。边(v, w)依附于顶点w和v,或者说边(v, w)和顶点v, w相关联。
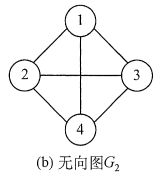
①不存在重复边
②不存在环
存在平行的边,即重复边
完全图(也称简单完全图)
Section titled “完全图(也称简单完全图)”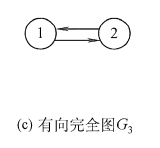

图的存储结构
Section titled “图的存储结构”顺序存储结构①邻接矩阵法
链式存储结构①邻接表法②十字链表法③临界多重表法
#define MAX_VERTEX_NUM 20#define INFINITY 32768typedef enum{DG,DN,UDG,UDN} GraphKind;typedef char VertexData; //假设存储结点类型为字符型typedef struct ArcNode{ AdjType adj; //对于无权图用1和0表示是否相邻,对带权图则为权值类型}ArcNode;typedef struct{ VertexData vertex[MAX_VERTEX_NUM]; ArcNode arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; int vexnum,arcnum;//图的顶点数和弧数 GraphKind kind;//图的种类标志}AdjMatrix;//求顶点的位置int LocateVertex(AdjMatrix *G,VertexData v){ int j = Error,k; for(k = 0;k < G->vexnum;k++){ if(G->vertex[k] == v){ j = k; break;//退出for循环 } } return(j);}//创建一个有向网int CreateDN(AdjMatrix *G){ int i,k,k,weight; VertexData v1,v2; scanf("%d%d",&G->arcnum,&G->vexnum);//输入顶点数和弧数 for(i = 0;i < G->vexnum;i++) for(j = 0;j < G->vexnum;j++) G->arcs[i][j].adj = INFINITY; for(i = 0;i < G->vexnum;i++) scanf('%c',&G->vertex[i]); for(k=0;k<G->arcnum;k++) { scanf("%c,%c,%d",&v1,&v2,&weight); /*输入一条弧的两个顶点及权值*/ i=LocateVex_M(G,v1); j=LocateVex_M(G,v2); G->arcs[i][j].adj=weight; /*建立弧*/ } return(Ok);}注意: ①在简单应用中,可直接用二维数组作为图的邻接矩阵(顶点信息等均可省略)。 ②当邻接矩阵中的元素仅表示相应的边是否存在时,EdgeType可定义为值为0和1的枚举类型。 ③无向图的邻接矩阵是对称矩阵,对规模特大的邻接矩阵可采用压缩存储。
④空间复杂度O(n^2)
⑤ 用邻接矩阵法存储图,很容易确定图中任意两个顶点之间是否有边相连。但是,要确定图中有多少条边,则必须按行、按列对每个元素进行检测,所花费的时间代价很大。 ⑥ 稠密图适合使用邻接矩阵的存储表示。
⑦对于无向图,由于它的邻接矩阵是对称矩阵,所以可以采用压缩存储法,(下三角),存储空间只要n(n-1)/2
邻接表表示法
Section titled “邻接表表示法”#define MAX_VERTEX_NUM 20typedef enum{DG,DN,UDG,UDN}typedef struct ArcNode{ int adjvex; //该弧指向顶点的位置 struct ArcNode *nextarc; OtherInfo info;//弧的相关信息,例如weight}ArcNode;typedef struct VertexNode{ VertexData data; ArcNode *firstarc;}VertexNode;typedef struct{ VertexNode vertex[MAX_VERTEX_NUM]; int vexnum,arcnum; GraphKind kind;}AdjList;#define MAXVEX 100 //图中顶点数目的最大值type char VertexType; //顶点类型应由用户定义typedef int EdgeType; //边上的权值类型应由用户定义/*边表结点*/typedef struct EdgeNode{ int adjvex; //该弧所指向的顶点的下标或者位置 EdgeType weight; //权值,对于非网图可以不需要 struct EdgeNode *next; //指向下一个邻接点}EdgeNode;
/*顶点表结点*/typedef struct VertexNode{ Vertex data; //顶点域,存储顶点信息 EdgeNode *firstedge //边表头指针}VertexNode, AdjList[MAXVEX];
/*邻接表*/typedef struct{ AdjList adjList; int numVertexes, numEdges; //图中当前顶点数和边数}查找(Searching):就是根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素( 或记录)。
查找表(Search Table):是由同一类型的数据元素(或记录)构成的集合。
关键字(Key):数据元素中唯一标识该元素的某个数据项的值,使用基于关键字的查找,查找结果应该是唯一的。例如,在由一个学生元素构成的数据集合中,学生元素中“学号”这一数据项的值唯一地标识一名学生。
静态查找表(Static Search Table):只作查找操作的查找表。
主要操作 查询某个“特定的”数据元素是否在查找表中。 检索某个“特定的”数据元素和各种属性。
动态查找表(Dynamic Search Table): 在查找过程中同时插入查找表中不存在的数据元素,或者从查找表中删除已经存在的某个数据元素。
主要操作 查找时插入不存在的数据元素。 查找时删除已存在的数据元素。
平均查找长度:在查找过程中,一次查找的长度是指需要比较的关键字次数,而平均查找长度,则是所有查找过程中进行关键字的比较次数的平均值,公式如下

typedef struct{ KeyType key; //关键词域 .....}ElemType;typedef struct{ ElemType *R; int length;}SSTable;SSTable ST;顺序查找算法
int Sequential_Search(int *a,int n,int key){ int i; a[0] = key;//设a[0]为关键字,称之为哨兵 i = n; while(a[i] != key) i--; return key;}查找效率高(对数级),但只适用于有序表的顺序存储结构
//非递归算法int Binary_Search(SSTable ST,ElemType key){ int low = 0,high = ST.length - 1,mid; while(low <= high){ mid = (low + high)/2; if(ST.R[mid].key == key) return key; else if(key < ST.R[mid].key) high = mid - 1; else low = mid + 1; }//while return 0;}//Search_Bin//递归算法/*二叉树的二叉链表结点结构定义*/typedef struct BiTNode{ int data; //结点数据 struct BiTNode *lchild, *rchild;} BiTNode, *Bitree;/*递归查找二叉排序树T中是否存在key指针f指向T的双亲,其初始调用值为NULL若查找成功,则指针p指向该数据元素结点,并返回TRUE否则指针p指向查找路径上访问的最后一个结点并返回FALSE*/bool SearchBST(BiTree T, int key, BiTree f, BiTree *p){ if(T == NULL){ *p = f; return FALSE; }else if(key == T->data){ //查找成功 *p = T; return TRUE; }else if(key < T->data){ return SearchBST(T->lchild, key, T, p); //在左子树继续查找 }else{ return SearchBST(T->rchild, key, T, p); //在右子树继续查找 }}/*当二叉排序树T中不存在关键字等于key的数据元素时插入key并返回TRUE,否则返回FALSE*/bool InsertBST(BiTree *T, int key){ BiTree p, s; if(!SearchBST(*T, key, NULL, &p)){ //查找不成功 s = (BiTree)malloc(sizeof(BiTNode)); s->data = key; s->lchild = s->rchild = NULL; if(!p){ *T = s; //插入s为新的根节点 }else if(key < p->data){ p->lchild = s; //插入s为左孩子 }else{ p->rchild = s; //插入s为右孩子 } return TRUE; }else{ return FALSE; //树种已有关键字相同的结点,不再插入 }}/*从二叉排序树中删除结点p,并重接它的左或右子树。*/bool Delete(BiTree *p){ BiTree q, s; if(p->rchild == NULL){ //右子树为空则只需重接它的左子树 q = p; p = p->lchild; free(q); }else if(p->lchild == NULL){ //左子树为空则只需重接它的右子树 q = p; p = p->rchild; free(q); }else{ //左右子树均不空 q = p; s = p->lchild; //先转左 while(s->rchild){//然后向右到尽头,找待删结点的前驱 q = s; s = s->rchild; } //此时s指向被删结点的直接前驱,p指向s的父母节点 p->data = s->data; //被删除结点的值替换成它的直接前驱的值 if(q != p){ q->rchild = s->lchild; //重接q的右子树 }else{ q->lchild = s->lchild; //重接q的左子树 } pree(s); } return TRUE;}/*若二叉排序树T中存在关键字等于key的数据元素时,则删除该数据元素结点,并返回TRUE;否则返回FALSE*/bool DeleteBST(BiTree *T, int key){ if(!T){ return FALSE; }else{ if(key == T->data){ //找到关键字等于key的数据元素 return Delete(T); }else if(key < T -> data){ return DeleteBST(T -> lchild, key); }else{ return DeleteBST(T -> rchild, key); } }}二叉排序树的优点明显,插入删除的时间性能比较好。而对于二叉排序树的查找,走的就是从根结点到要查找的结点的路径,其比较次数等于给定值的结点在二叉排序树的层数。极端情况,最少为1次,即根结点就是要找的结点,最多也不会超过树的深度。也就是说,二叉排序树的查找性能取决于二叉排序树的形状。可问题就在于,二叉排序树的形状是不确定的。 例如{ 62 , 88 , 58 , 47 , 35 , 73 , 51 , 99 , 37 , 93 } {62,88,58,47,35,73,51,99,37,93}{62,88,58,47,35,73,51,99,37,93}这样的数组,我们可以构建如下左图的二叉排序树。但如果数组元素的次序是从小到大有序,如{35,37,47,51,58,62,73,88,93,99},则二叉排序树就成了极端的右斜树,如下面右图的二叉排序树:
最好的情况 & 最坏的情况
左右子树深度之差小于等于1的树
平衡二叉树的查找
Section titled “平衡二叉树的查找”平衡二叉树的插入
Section titled “平衡二叉树的插入”RR RL LL LR
