进制

四种进制介绍

1. 二进制 以0b或0B开头

2. 十进制

3. 八进制 以0开头

4. 十六进制 用0-9，A-F(不区分大小写)表示，以0x或0X开头

   int n1 = 0b1010;
   int n2 = 1010;
   int n3 = 01010;
   int n4 = 0x1010;

n进制与10进制的转换

①将n进制数转换为10进制数的公式为：

其中， 表示第 位上的数字。

②将10进制数转换为n进制数的公式为：

将10进制数不断除以n，得到的余数即为n进制数的每一位数字，直到商为0为止。将余数倒序排列即可得到n进制数。

例如，将10进制数 123 转换为 2进制数：

• 123 ÷ 2 = 61 余 1
• 61 ÷ 2 = 30 余 1
• 30 ÷ 2 = 15 余 0
• 15 ÷ 2 = 7 余 1
• 7 ÷ 2 = 3 余 1
• 3 ÷ 2 = 1 余 1
• 1 ÷ 2 = 0 余 1

所以，10进制数123转换为2进制数为 。

8进制、16进制与2进制的转换

①将N进制数转换为2进制数的公式为：

1. 从低位开始将二进制数每 位一组进行分组，不足 位的在前面补0，得到若干组二进制数。
2. 将每组二进制数转换为十进制数。
3. 将每个十进制数转换为N进制数，得到若干组N进制数。
4. 将所有N进制数连接起来，即为所求的N进制数。

②将N进制数转换为2进制数的公式为：

1. 将N进制数每一位转换为对应的十进制数。
2. 将每个十进制数转换为二进制数，得到若干组二进制数。
3. 将每个二进制数不足 位的在前面补0，得到若干组等长的二进制数。
4. 将所有等长的二进制数连接起来，即为所求的二进制数。
   • n的取值如下:
   • 要将8进制数转换为二进制数，则每1位转换为3位二进制数
   • 要将16进制数转换为二进制数，则每1位转换为4位二进制数

位运算

补码、原码、反码

对于有符号的而言

1. 二进制的最高位是符号位：0表示整数，1表示负数
2. 正数的原码，反码，补码都一样(三码合一)
3. 负数的反码 = 它的原码符号位不变，其它位取反（0->1,1->0)
4. 负数的补码 = 负数的反码 + 1，负数的反码 = 负数的补码 - 1
5. 0的反码，补码都是0
6. java没有无符号数，换言之，java中的数都是有符号的
7. 在计算机进行各种运算的时候，都是以补码的方式来运算的(因为补码统一了正负数)
8. 当我们看运算结果的时候，要看它的原码

位运算符

1. 按位与&：两位均为1时为1，否则为0

2. 按位或|：两位有一个为1则为1，否则为0

3. 按位异或^：两位不同则为1，否则为0

4. 按位取反~：0->1，1->0

5. 算数右移>>：低位溢出，符号位不变，并用符号位补溢出的高位

6. 算数左移<<：符号位不变，低位补0

7. 逻辑右移/无符号右移>>>：低位溢出，高位补0

   int a = 1 >> 2; //算数右移两位，本质：1 / 2 / 2 = 0
   1 => 00000000 00000000 00000000 00000001
   1 >> 2 => 00000000 00000000 00000000 00000000
   int c = 1 << 2; //算数左移两位，本质：1 * 2 * 2 = 4
   1 << 2 => 00000000 00000000 00000000 00000100

[!abstract] Bit

• 位（bit）：又名比特，表示二进制位，是计算中内部数据储存的最小单位。一个二进制位只能表示 0 和 1 两种状态。
• 字节（byte）：计算机中处理数据的基本单位。一个字节等于八位（1Byte = 8bit）
• 字（word）：计算机进行数据处理时，一次存取、加工和传送的数据长度。在常见的计算机编码格式下，一个字等于两个字节（十六位）（1word = 2Byte = 16bit）

快速幂算法

时间复杂度

public long fastPowerMode(long basenumber, int exponent) {
    long res = 1;
    for (; exponent > 0; exponent >>= 1) {
        if (exponent % 2 == 1) {
            res = (res * basenumber)
        }
        basenumber = (basenumber * basenumber);
    }
    return res;
}

public long fastPowerMode(long basenumber, int exponent, int mod) {
    long res = 1;
    for (; exponent > 0; exponent >>= 1) {
        if (exponent % 2 == 1) {
            res = (res * basenumber) % mod;
        }
        basenumber = (basenumber * basenumber) % mod;
    }
    return res;
}

求>=cap 中 2 的幂的最小值

static final int tableSizeFor(int cap) {
        int n = cap - 1;
        n |= n >>> 1;
        n |= n >>> 2;
        n |= n >>> 4;
        n |= n >>> 8;
        n |= n >>> 16;
        return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
    }

2 的整数次幂的数，最高位是 1，其余位都是 0，例如 16 的二进制位:10000,那么 15 就是1111，所以反复或的操作就是不断地把每个位数都变成 1，最后+1 就变成了最近的二的整数次幂的数

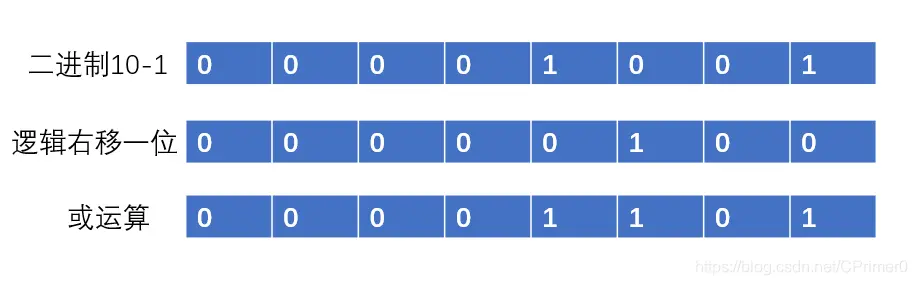
第一次或操作：向右移动一位，最高有效位 1 也会向右移动一位，我们知道或操作有 1 就变成 1，所以最高两位有效位都会变成 1

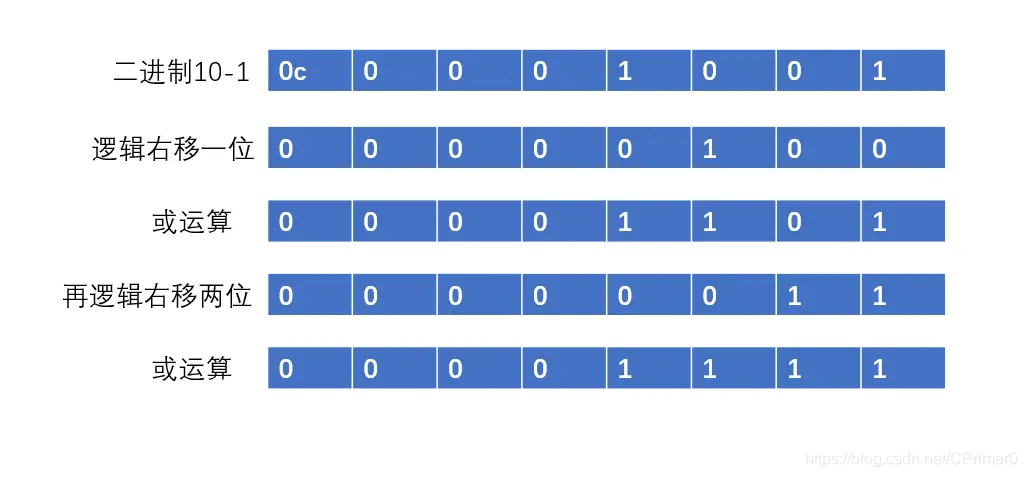
第二次或操作：当再向右移动两位，相当于把第一步的高两位向后移动两位，所以或运算后，四位都是 1

此时已经完成操作了，再移动结果不改变，最多移动 16 位，是因为 int4 个子节，32 位，最多移动高 16 位到低 16 位就能完成操作

所以当位运算操作完之后，(n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;这里如果不超过最大值就返回 n+1，例子中返回 15+1 = 16